集合
集合运算:并,交,补
集合代数:德摩尔定律即补集的并集等于原集的交集反之亦然
概率模型
样本空间:空间内结果相斥
概率率 :1.非负性,2.可加性,3.归一化
概率律性质
若$A\subset B,则P(A) \leq P(B) $
P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B ) P(A \cup B )=P(A)+P(B)-P(A\cap B) P ( A ∪ B ) = P ( A ) + P ( B ) − P ( A ∩ B )
P ( A ∪ B ) ≤ P ( A ) + P ( B ) P(A\cup B)\leq P(A)+P(B) P ( A ∪ B ) ≤ P ( A ) + P ( B )
P ( A ∪ B ∪ C ) = P ( A ) + P ( A c ∩ B ) + P ( A c ∩ B c ∩ C ) P(A \cup B \cup C)=P(A)+P(A^c \cap B)+P(A^c\cap B^c \cap C) P ( A ∪ B ∪ C ) = P ( A ) + P ( A c ∩ B ) + P ( A c ∩ B c ∩ C )
序贯模型:针对有序事件
离散模型:样本空间内由有限个可能的结果组成:P ( s 1 , s 2 , ⋯ , s n ) = P ( s 1 ) + P ( s 2 ) + ⋯ + P ( s n ) P({s_1,s_2,\dotsb,s_n})=P(s_1)+P(s_2)+\dotsb+P(s_n) P ( s 1 , s 2 , ⋯ , s n ) = P ( s 1 ) + P ( s 2 ) + ⋯ + P ( s n )
连续模型:试验的样本空间为连续集合
贝特斯悖论:对于同一事件不同的模型导致结论不确定。例:三门问题。
条件概率:P ( A ∣ B ) = 事件 A ∩ B 的试验结果数 事件 B 发生的试验结果数 = P ( A ∩ B ) P ( B ) P(A|B)=\frac{事件A\cap B的试验结果数}{事件B发生的试验结果数}=\frac{P(A\cap B)}{P(B)} P ( A ∣ B ) = 事 件 B 发 生 的 试 验 结 果 数 事 件 A ∩ B 的 试 验 结 果 数 = P ( B ) P ( A ∩ B )
乘法规则:P ( ∩ i = 1 n A i ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 ∩ A 2 ) ⋯ P ( A n ∣ ∩ i = 1 n − 1 A i ) P( \cap _{i=1}^nA_i)=P(A_1)P(A_2|A_1)P(A_3|A_1\cap A_2)\dotsb P(A_n|\cap_{i=1}^{n-1}A_i) P ( ∩ i = 1 n A i ) = P ( A 1 ) P ( A 2 ∣ A 1 ) P ( A 3 ∣ A 1 ∩ A 2 ) ⋯ P ( A n ∣ ∩ i = 1 n − 1 A i )
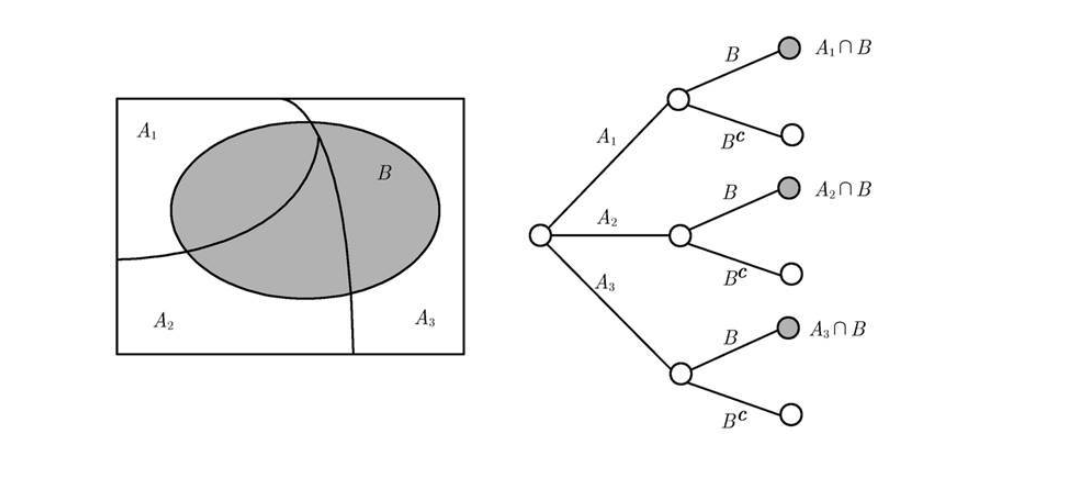
全概率定理:P ( B ) = ∑ i = 1 n P ( A n ∩ B ) P(B)= \sum_{i=1}^n P(A_n \cap B) P ( B ) = ∑ i = 1 n P ( A n ∩ B )
与条件概率的差异
贝叶斯准则:设A 1 , A 2 , ⋯ , A n A_1,A_2,\dotsb,A_n A 1 , A 2 , ⋯ , A n
不是很重要的推导过程P ( A i ∣ B ) = P ( A i ∩ B ) P ( B ) = P ( A i ) P ( B ∣ A i ) P ( A 1 ) P ( B ∣ A 1 ) + ⋯ + P ( A n ) P ( B ∣ A n ) P(A_i|B)=\frac{P(A_i\cap B)}{P(B)}=\frac{P(A_i){P(B|A_i)} }{P(A_1)P(B|A_1)+\dotsb +P(A_n)P(B|A_n) } P ( A i ∣ B ) = P ( B ) P ( A i ∩ B ) = P ( A 1 ) P ( B ∣ A 1 ) + ⋯ + P ( A n ) P ( B ∣ A n ) P ( A i ) P ( B ∣ A i )
将P ( A ∣ B ) P(A|B) P ( A ∣ B ) P ( B ∣ A ) P(B|A) P ( B ∣ A )
独立性:P ( A ∣ B ) = P ( A ) ⟺ P ( A ∩ B ) = P ( A ) P ( B ) P(A|B)=P(A)\iff P(A\cap B)=P(A)P(B) P ( A ∣ B ) = P ( A ) ⟺ P ( A ∩ B ) = P ( A ) P ( B ) 其中P ( B ) > 0 P(B)>0 P ( B ) > 0
条件独立:P ( A ∩ B ∣ C ) = P ( A ∣ C ) P ( B ∣ C ) ⟺ P ( A ∣ B ∩ C ) = P ( A ∣ C ) P(A\cap B|C)=P(A|C)P(B|C)\iff P(A|B\cap C)=P(A|C) P ( A ∩ B ∣ C ) = P ( A ∣ C ) P ( B ∣ C ) ⟺ P ( A ∣ B ∩ C ) = P ( A ∣ C )
一组事件独立:任意两两事件且所有事件相互独立
P ( X ∈ B ) = ∫ b f ( x ) d x P(X\in B)=\displaystyle\int_b{f(x)}{dx} P ( X ∈ B ) = ∫ b f ( x ) d x f ( x ) f(x) f ( x )
端点无用:P ( X = a ) = ∫ a a f ( x ) d x = 0 P(X=a)=\displaystyle\int_a^a{f(x)}{dx}=0 P ( X = a ) = ∫ a a f ( x ) d x = 0 P ( a ≤ X ≤ b ) = P ( a < X ≤ b ) = P ( a ≤ X < b ) = P ( a < X < b ) P(a\leq X\leq b)=P(a < X\leq b)=P(a\leq X < b)=P(a < X < b) P ( a ≤ X ≤ b ) = P ( a < X ≤ b ) = P ( a ≤ X < b ) = P ( a < X < b )
关于PDF性质的小结:
设 X X X f X ( x ) f_X(x) f X ( x ) f X ( x ) ≥ 0 f_X(x)\geq 0 f X ( x ) ≥ 0 且可以大于1
∫ − ∞ ∞ f X ( x ) d x = 1 \int^\infty_{-\infty}f_X(x)\text{d}x=1 ∫ − ∞ ∞ f X ( x ) d x = 1
设 δ 是一个充分小的正数, 则 P ( [ x , x + δ ] ) ≈ f X ( x ) ⋅ δ \text{P}([x,x+\delta])\approx f_X(x)\cdot\delta P ( [ x , x + δ ] ) ≈ f X ( x ) ⋅ δ 其中P ( [ x , x + δ ] ) \text{P}([x,x+\delta]) P ( [ x , x + δ ] ) f X ( x ) f_X(x) f X ( x )
对任何实数轴上的子集B B B P ( X ∈ B ) = ∫ B f X ( x ) d x {\rm P}(X\in{B})=\displaystyle\int_{B}{f}_X(x)dx P ( X ∈ B ) = ∫ B f X ( x ) d x
常见分布列
均匀随机变量:即f ( X ) f(X) f ( X ) [ a , b ] [a,b] [ a , b ]
指数随机变量:$f_X(x)=\begin{cases}
\lambda e^{-\lambda x},若x\geq 0 \
0 ,其他\end{cases}$
正态随机变量:f X ( x ) = 1 2 π σ e − ( x − μ ) 2 / ( 2 σ 2 ) , f_X(x)=\frac1{\sqrt{2\pi}\sigma}{\rm e}^{-(x-\mu)^2/(2\sigma^2)}, f X ( x ) = 2 π σ 1 e − ( x − μ ) 2 / ( 2 σ 2 ) ,
线性变换之下,随机变量的正态性保持不变,体现在方差和期望
正态随机变量 Y 的期望μ \mu μ σ 2 \sigma^2 σ 2
结合上述性质,可以将非标准快速转换为标准,再利用标准正态速查表进行快速计算正态分布的结果
期望:
期望:我们把p x × x px\times x p x × x M = E [ X ] M=E[X] M = E [ X ]
离散 期望值为M = m 1 k 1 + m 2 k 2 + ⋯ + m n k n k M=\frac {m_1k_1+m_2k_2+\dots+m_nk_n}{k} M = k m 1 k 1 + m 2 k 2 + ⋯ + m n k n k k k k i k ≈ p i \frac {k_i}{k} \approx p_i k k i ≈ p i E [ X ] = ∑ x x p X ( x ) E[X]=\sum_x xp_X(x) E [ X ] = ∑ x x p X ( x )
连续随机期望 依据定义:E [ X ] = ∫ − ∞ ∞ x f X ( x ) d x . {\rm E}[X]=\int_{-\infty}^{\infty}xf_X(x){d}x. E [ X ] = ∫ − ∞ ∞ x f X ( x ) d x .
通常我们会将其看作分布列的重心
期望规则
随机变量Y = a X + b Y=aX+b Y = a X + b E [ Y ] = a E [ X ] + b , v a r [ Y ] = a 2 v a r ( X ) E[Y]=aE[X]+b,var[Y]=a^2var(X) E [ Y ] = a E [ X ] + b , v a r [ Y ] = a 2 v a r ( X )
v a r ( X ) = E [ X 2 ] − ( E [ X ] ) 2 var(X)=E[X^2]-(E[X])^2 v a r ( X ) = E [ X 2 ] − ( E [ X ] ) 2
条件期望:根据定义E [ X ∣ A ] = ∑ x x p X ∣ A ( x ) {\rm E}[X|A]=\sum_xxp_{X|A}(x) E [ X ∣ A ] = ∑ x x p X ∣ A ( x )
方差
方差:记作v a r [ X ] var[X] v a r [ X ] v a r [ X ] = E [ ( X − E [ X ] ) 2 ] var[X]=E[(X-E[X])^2] v a r [ X ] = E [ ( X − E [ X ] ) 2 ]
标准差:σ X = var ( X ) . \sigma_X=\sqrt{\text{var}(X)}. σ X = var ( X ) .
连续随机方差:var ( X ) = E [ ( X − E [ X ] ) 2 ] = ∫ − ∞ + ∞ ( x − E [ X ] ) 2 f X ( x ) d x \text{var}(X)=E[(X-E[X])^2]=\int_{-\infty}^{+\infty}(x-E[X])^2f_X(x)dx var ( X ) = E [ ( X − E [ X ] ) 2 ] = ∫ − ∞ + ∞ ( x − E [ X ] ) 2 f X ( x ) d x
两者都是衡量X X X
常用的随机变量的均值和方差
伯努利随机变量:E [ X ] = 1 ⋅ p + 0 ⋅ ( 1 − p ) = p \\E[X]=1\cdot{p}+0\cdot(1-p)=p\\ E [ X ] = 1 ⋅ p + 0 ⋅ ( 1 − p ) = p E [ X 2 ] = 1 2 ⋅ p + 0 2 ⋅ ( 1 − p ) = p {\rm E}[X^2]=1^2\cdot{p}+0^2\cdot(1-p)=p\\ E [ X 2 ] = 1 2 ⋅ p + 0 2 ⋅ ( 1 − p ) = p var ( X ) = E [ X 2 ] − ( E [ X ] ) 2 = p − p 2 = p ( 1 − p ) \text{var}(X)={\rm E}[X^2]-({\rm E}[X])^2=p-p^2=p(1-p) var ( X ) = E [ X 2 ] − ( E [ X ] ) 2 = p − p 2 = p ( 1 − p )
离散均匀 随机变量E [ X ] = a + b 2 , v a r [ X ] = ( b − a ) ( b − a + 2 ) 12 \\E[X]=\frac{a+b}{2},\\var[X]=\frac{(b-a)(b-a+2)}{12} E [ X ] = 2 a + b , v a r [ X ] = 1 2 ( b − a ) ( b − a + 2 )
二项分布式:E [ X ] = n p \\E[X]=np E [ X ] = n p var ( X ) = ∑ i = 1 n var ( X i ) = n p ( 1 − p ) \\\text{var}(X)=\sum_{i=1}^n\text{var}(X_i)=np(1-p) var ( X ) = ∑ i = 1 n var ( X i ) = n p ( 1 − p )
泊松随机变量:E [ X ] = λ E[X]=\lambda E [ X ] = λ v a r ( X ) = E [ Y 2 ] − ( E [ Y ] ) 2 = λ ( λ + 1 ) − λ 2 = λ var(X)=E[Y^2]-(E[Y])^2=\lambda(\lambda+1)-\lambda^2=\lambda v a r ( X ) = E [ Y 2 ] − ( E [ Y ] ) 2 = λ ( λ + 1 ) − λ 2 = λ
几何变量:E [ X ] = 1 p {\rm E}[X]=\frac 1 p E [ X ] = p 1
var ( X ) = E [ X 2 ] − ( E [ X ] ) 2 = 2 p 2 − 1 p − 1 p 2 = 1 − p p 2 . \\\text{var}(X)={\rm E}[X^2]-({\rm E}[X])^2=\frac2{p^2}-\frac1p-\frac1{p^2}=\frac{1-p}{p^2}. var ( X ) = E [ X 2 ] − ( E [ X ] ) 2 = p 2 2 − p 1 − p 2 1 = p 2 1 − p .
均匀随机变量:
E [ X ] = a + b 2 E[X]=\frac{a+b}{2}\\ E [ X ] = 2 a + b var ( X ) = E [ X 2 ] − ( E [ X ] ) 2 = a 2 + a b + b 2 3 − ( a + b ) 2 4 = ( b − a ) 2 12 . \text{var}(X)={\rm E}[X^2]-({\rm E}[X])^2=\frac{a^2+ab+b^2}3-\frac{(a+b)^2}4=\frac{(b-a)^2}{12}. var ( X ) = E [ X 2 ] − ( E [ X ] ) 2 = 3 a 2 + a b + b 2 − 4 ( a + b ) 2 = 1 2 ( b − a ) 2 .
指数随机变量:E [ X ] = 1 λ var ( X ) = 1 λ 2 {\rm E}[X]=\frac1\lambda\quad\text{var}(X)=\frac1{\lambda^2} E [ X ] = λ 1 var ( X ) = λ 2 1
正态分布:E [ X ] = μ , var ( X ) = σ 2 . {\rm E}[X]=\mu,\quad\text{var}(X)=\sigma^2. E [ X ] = μ , var ( X ) = σ 2 .
大数定律:所以当 n → ∞ n\to\infty n → ∞ M n M_n M n M n M_n M n μ \mu μ 大数定律 的内容,即随机变量序列 M n M_n M n μ \mu μ
中心极限定理:用 S n S_n S n n μ n\mu n μ σ n \sigma\sqrt{n} σ n Z n = S n − n μ σ n . Z_n=\frac{S_n-n\mu}{\sigma\sqrt{n} }. Z n = σ n S n − n μ . E [ Z n ] = 0 , var ( Z n ) = 1. {\rm E}[Z_n]=0, \ \ \ \text{var}(Z_n)=1. E [ Z n ] = 0 , var ( Z n ) = 1 . Z n Z_n Z n Z n Z_n Z n n n n Z n Z_n Z n
马尔可夫不等式:P ( X ≥ a ) ≤ E [ X ] a {\rm P}(X\geq a)\leq \frac{ {\rm E}[X]}{a} P ( X ≥ a ) ≤ a E [ X ]
切比雪夫不等式:随机变量 X 的均值为 μ \mu μ σ 2 \sigma^2 σ 2 c c%3e0 c P ( ∣ X − μ ∣ ≥ c ) ≤ σ 2 c 2 {\rm P}(|X-\mu|\geq c)\leq \frac{\sigma^2}{c^2} P ( ∣ X − μ ∣ ≥ c ) ≤ c 2 σ 2
通过上述四个理论,大数定理和中心极限提供了数学理论基础,而马尔可夫不等式和切比雪夫不等式则计算出来一定的概率上限。
古典模型:P ( A ) = 含事件 A 的结果数 n P(A)=\frac{含事件A的结果数}{n} P ( A ) = n 含 事 件 A 的 结 果 数
概率律的所有性质都在后续有应用,基于不同的模型。
条件概率也满足概率律的所有性质:P ( A ∣ C ∪ B ∣ C ) ≤ P ( A ∣ C ) + P ( B ∣ C ) P(A|C\cup B|C)\leq P(A|C)+P(B|C) P ( A ∣ C ∪ B ∣ C ) ≤ P ( A ∣ C ) + P ( B ∣ C )
试着使用现实意义进行描述贝叶斯准则:通过事目标件B在特定条件下的发生概率,来反推出事件B在无条件或者特定样本空间下的概率。即在通过结果来反推出发生原因的概率。
继续不是很重要的推导过程,中间用到条件概率的乘法法则:P ( A ∩ B ∣ C ) = P ( A ∩ B ∩ C ) P ( C ) = P ( C ) P ( B ∣ C ) P ( A ∣ B ∩ C ) P ( C ) = P ( B ∣ C ) P ( A ∣ B ∩ C ) ⟺ P ( B ∣ C ) P ( A ∣ B ∩ C ) = P ( A ∣ C ) P ( B ∣ C ) ⟺ P ( A ∣ B ∩ C ) = P ( A ∣ C ) P(A\cap B|C)=\frac{P(A\cap B \cap C)}{P(C)}=\frac{P(C)P(B|C)P(A|B\cap C)}{P(C)}=P(B|C)P(A|B \cap C) \iff P(B|C)P(A|B \cap C)=P(A|C)P(B|C) \iff P(A|B\cap C)=P(A|C) P ( A ∩ B ∣ C ) = P ( C ) P ( A ∩ B ∩ C ) = P ( C ) P ( C ) P ( B ∣ C ) P ( A ∣ B ∩ C ) = P ( B ∣ C ) P ( A ∣ B ∩ C ) ⟺ P ( B ∣ C ) P ( A ∣ B ∩ C ) = P ( A ∣ C ) P ( B ∣ C ) ⟺ P ( A ∣ B ∩ C ) = P ( A ∣ C )
组合数即意味着含有次序
试图证明泊松变量和二项随机变量的逼近:设n → ∞ , p → 0 n\to \infty,p\to 0 n → ∞ , p → 0 n p = λ np= \lambda n p = λ k(1-p) {n-k}\end{align*}中 中 中 得到只剩下 得到只剩下 得 到 只 剩 下 的式子,求极限。总结下对应意义就是在试验次数 的式子,求极限。总结下对应意义就是在试验次数 的 式 子 , 求 极 限 。 总 结 下 对 应 意 义 就 是 在 试 验 次 数 很大的情况下, 很大的情况下, 很 大 的 情 况 下 , 很小,则无限接近二项随机变量。现实意义就是:如果大规模事件出现小概率事件的次数 很小,则无限接近二项随机变量。现实意义就是:如果大规模事件出现小概率事件的次数 很 小 , 则 无 限 接 近 二 项 随 机 变 量 。 现 实 意 义 就 是 : 如 果 大 规 模 事 件 出 现 小 概 率 事 件 的 次 数
试着使用重心理论去理解,图像的增大和缩小会影响其重心,和X X X
依旧不是很重要的证明过程:直接使用定义法:
\begin{align*}\text{var}(X)&=\sum_x\left(x-{\rm E}[X]\right)^2p_X(x)\\&=\sum_x\left(x^2-2x{\rm E}[X]+({\rm E}[X])^2\right)p_X(x)\\&=\sum_xx^2p_X(x)-2{\rm E}[X]\sum_xxp_X(x)+({\rm E}[X])^2\sum_xp_X(x)\\&={\rm E}[X^2]-2({\rm E}[X])^2+({\rm E}[X])^2\\&={\rm E}[X^2]-({\rm E}[X])^2.\end{align*}
随机变量 X 和 Y 称为相互独立 的随机变量, 若它们满足p X , Y ( x , y ) = p X ( x ) p Y ( y ) p_{X,Y}(x,y)=p_X(x)p_Y(y) p X , Y ( x , y ) = p X ( x ) p Y ( y ) X = x X=x X = x Y = y Y=y Y = y p X , Y ( x , y ) = p X ∣ Y ( x ∣ y ) p Y ( y ) p_{X,Y}(x,y)=p_{X|Y}(x|y)p_Y(y) p X , Y ( x , y ) = p X ∣ Y ( x ∣ y ) p Y ( y ) X X X Y Y Y p X ∣ Y ( x ∣ y ) = p X ( x ) p_{X|Y}(x|y)=p_X(x) p X ∣ Y ( x ∣ y ) = p X ( x ) p Y ( y ) > 0 p_Y(y)>0 p Y ( y ) > 0 ( P ( A ) 必须大于 0 ! ) ({\rm P}(A) 必须大于0!) ( P ( A ) 必 须 大 于 0 ! ) Y Y Y A A A
满足概率律
线性变换之下随机变量的正态性保持不变:设 X 是正态随机变量, 其均值为μ \mu μ σ 2 \sigma^2 σ 2 a ≠ 0 a\not=0 a = 0 b b b Y = a X + b Y=aX+b Y = a X + b E [ Y ] = a μ + b , var ( Y ) = a 2 σ 2 . {\rm E}[Y]=a\mu+b,\quad\text{var}(Y)=a^2\sigma^2. E [ Y ] = a μ + b , var ( Y ) = a 2 σ 2 .


 ,看完之后,我只想说:“日你妈,退钱”
,看完之后,我只想说:“日你妈,退钱”