python 线性回归-最小二乘法

发表于 2022-12-28 阅读次数：本文字数： 1.3k 阅读时长 ≈ 5 分钟

python 线性回归-最小二乘法

数学基础

说起线性回归，大多数人的反馈就如同下面2张图片一样，通过一些数据点的拟合，选取出一个最简单的 $y=ax+b$ ，来最接近所有数据截距最短。

线性回归1

线性回归2

这里就要提出一个问题，我们要如何取舍 $a,b$ 使得这条直线最接近大多数的点，使得这条直线能够最好的满足大多数点的位置，使我们达到模拟的目的。

假设数据集为(即对应的 $x,y$ 的实际合计)：

\mathcal{D}={(x_1, y_1),(x_2, y_2),\cdots,(x_N, y_N)}

后面我们记(这里将 $x,y$ 单独独立出来成一个矩阵，方便后续计算计算，且注意，这里的 $x$ 可以是一个多元矩阵，但是必须注意需要将其转置成纵列，每一行都是多元x的数据集，方便后续计算，且在python的sklearn里面也是需要将x转置成纵列。)：

X=(x_1,x_2,\cdots,x_N)^T=\begin{pmatrix} x_1^T\\x_2^T\\\vdots\\x_N^T \end{pmatrix}=\begin{pmatrix} x_{11}& x_{12}&\cdots&x_{1p}\\ x_{21}&x_{22}&\cdots&x_{2p}\\ \vdots&\vdots&&\vdots\\ x_{n1}&x_{n2}&\cdots&x_{np} \end{pmatrix}_{N\times p}\\ Y=(y_1,y_2,\cdots,y_N)^T=\begin{pmatrix} y_1\\y_2\\\vdots\\y_N \end{pmatrix}_{N\times1}

其中N代表的是 $x$ 的数据集长度，而 $p$ 代表 $x$ 的多元性。

线性回归假设：

f(w)=w^Tx

注意这里后面有个b，但是为了方便表示，全部归结到前面

这里，我们将线性回归函数产生的点和实际点的差距记为损失，我们可以使用最小二乘法来定义损失函数。

L(w)=\sum\limits_{i=1}^N||w^Tx_i-y_i||^2

这里双竖线代表的是矩阵的绝对值符号

展开得到涉及到矩阵的计算法则，不懂去补，不过不会影响到理解 ：

\begin{align} L(w)&=(w^Tx_1-y_1,\cdots,w^Tx_N-y_N)\cdot (w^Tx_1-y_1,\cdots,w^Tx_N-y_N)^T\\ &=(w^TX^T-Y^T)\cdot (Xw-Y)\\&=w^TX^TXw-Y^TXw-w^TX^TY+Y^TY\\ &=w^TX^TXw-2w^TX^TY+Y^TY \end{align}

最小化这个值的,即对 $w$ 进行求导继续矩阵的求导：

\begin{align} \hat{w}=\mathop{argmin}\limits_wL(w)&\longrightarrow\frac{\partial}{\partial w}L(w)=0\\ &\longrightarrow2X^TX\hat{w}-2X^TY=0\\ &\longrightarrow \hat{w}=(X^TX)^{-1}X^TY\\&\longrightarrow \hat{w}=X^+Y \\&X^+为伪逆 \end{align}

总结：最小二乘法：我们通过计算所有截距的乘积的最小值来计算出最合适的一条直线，这同时也是最小二乘法在二维平面内的几何意义。

如果将 $x$ 看作多维空间,会变成是一条直线对 $x$ 维空间内的投影距离最小，理解就行这里涉及到向量空间：

f(w)=w^Tx = x^T\beta

python应用

上面说明了数学原理，现在到了实际的python应用，具体代码如下


%matplotlib inline

import matplotlib.pyplot as plt

import seaborn as sns;sns.set()

import numpy as np



#导入必须的包

rng=np.random.RandomState(1)    #设定随机种子，保证每次执行的结果都意志

x=10*rng.rand(50)   #随机生成50个数值

y=2*x-5+rng.randn(50)   #随机产生50个标准正态分布的随机数的函数



plt.scatter(x,y)    #简单的描绘一下

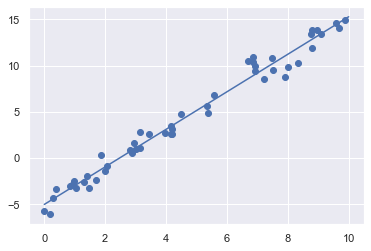
得到如下的图片

线性回归1

接下来就是对这份数据进行预测：


from sklearn.linear_model import LinearRegression #导入线性代数的包

model=LinearRegression(fit_intercept=True) #创建一个模型

model.fit(x[:,np.newaxis],y) #这里需要注意我们使用x[:,np.newaxis]，将x进行转置，至于为啥，可以看上面数学基础，我们将这个作为一个y=ax+b的，所以N=50，p=1，需要设定成50行1列的矩阵输入进行预测，

xfit=np.linspace(0,10,1000) #这里创建了一个0到10，之间1000个相邻的数据

yfit=model.predict(xfit[:,np.newaxis])#用1000个数据输入到预测模型，输出新的y



plt.scatter(x,y)

plt.plot(xfit,yfit)#剩下的就是看预测的y和实际的差距

线性回归2

到此算是一个简单的模型搭建完毕，那么有些人如果说，我得数据是2元的，甚至是多元的，那么该如何：

还是一样，我们需要创建一个数据，这次是2元的，即2个未知数，并且设定一个方程给他。


rng=np.random.RandomState(2)

x1=10*rng.rand(50)

x2=20*rng.rand(50)

y=4*x1+5*x2-10+rng.randn(50) #一个简单的二元一次方程

x_new=np.stack([x1, x2], axis=1) #我们需要输入一个N=50，p=2的50行2列的矩阵，其中50行代表数据量，2列代表的是2个未知数

#然后还是继续训练模型

model2=LinearRegression(fit_intercept=True) #注意命名新的模型

model2.fit(x_new,y)



print(model2.coef_[0],model2.coef_[1],model2.intercept_) #由于2元一次方程没有比较好的图片呈现形式，我们可以直接输出对应的斜率和截距，即y=ax+b的a和b，进行和原本数据对比。

20221228161724

所以数据精度还是可以的，但是前提这个是一个一次方程。

python 线性回归-最小二乘法

数学基础

总结：最小二乘法：我们通过计算所有截距的乘积的最小值来计算出最合适的一条直线，这同时也是最小二乘法在二维平面内的几何意义。

python应用

总结：最小二乘法可以说的上是最基础也是最简单的数据拟合，但是其中原理可一点都不简单，所以还是需要多加应用和学习。