概率论有感

《概率导论》终于是读完了，如果说前面几个章节还算是我能够自己学习并且理解的话，到了后面已经完全的变为了纯数学概念的转换。无论是贝叶斯还是切比雪夫链，我光是看都看不懂，于是，我的建议是后面的几个张章节的衍生，还是自己另外找视频辅助。书本确实比较符合我们的思维速度，所以一开始建立基础知识的时候，看书可以帮助我们更好的理解，但是到了后面，尤其是数学，很多时候简单的一个符号就需要大量的计算和理解，所以我们需要视频辅助，根据视频讲解的内容让我们更好的理解这些概念。

这就像是我最近在辅导孩子的数学作业一样的感受，如果说我在孩子这个年纪，那些数学的方法和思维让我想，凭空想出来，说实话我想不出来，而且就算是想出来了，没有经常使用，随着时间或者当时的状态，我估计我也搞不清楚这些概念和规律的。但是那天教学孩子的时候，我在自己做了两道题之后就发现了其中的奥妙，然后花费2个下午的时间将这个奥妙分解成孩子能够理解的语言，简单而言就是通过将分数乘法转变为分数减法来计算有规律的分数的n项之和。这种题目一般不会是数学卷子的最后大题，但是会是倒数第二道那种地位，属于不是强制要求，但是考验你思维灵活度的题目。如果你理解了，看懂了，那么这种题目做起来就得心应手，不会，也不会对你的基础知识有太多的影响。

现在想来，数学就是这么一样东西。数学是一个不定的学科，他的高阶题目是没有一个定论的。是，有时候是有比如取对数将乘法变为加减这种小技巧，但是正如之前所说，这些小技巧一般对应的是特殊的题目，不具备广泛性，所以，很多时候你光记住技巧是没有用处的，更加需要的是你的思维。而数学的一个基本思维就是：将不知道的问题变为已知的问题。就好像笑话说的：一个数学家看到房子着火的话会找来消防队，如果这个房子倒塌了，那么数学家就会把房子点着火，然后再来找到消防队。这就是一个基本的数学思维，万剑归宗般的一套解决理论。那么我们是记不住那一万把剑的，所以我们只需要记住那个思维就行，而如何记住这些思维：我觉得就是刷题。遇见的事务多了，你就自然而然的了解其中的真谛。

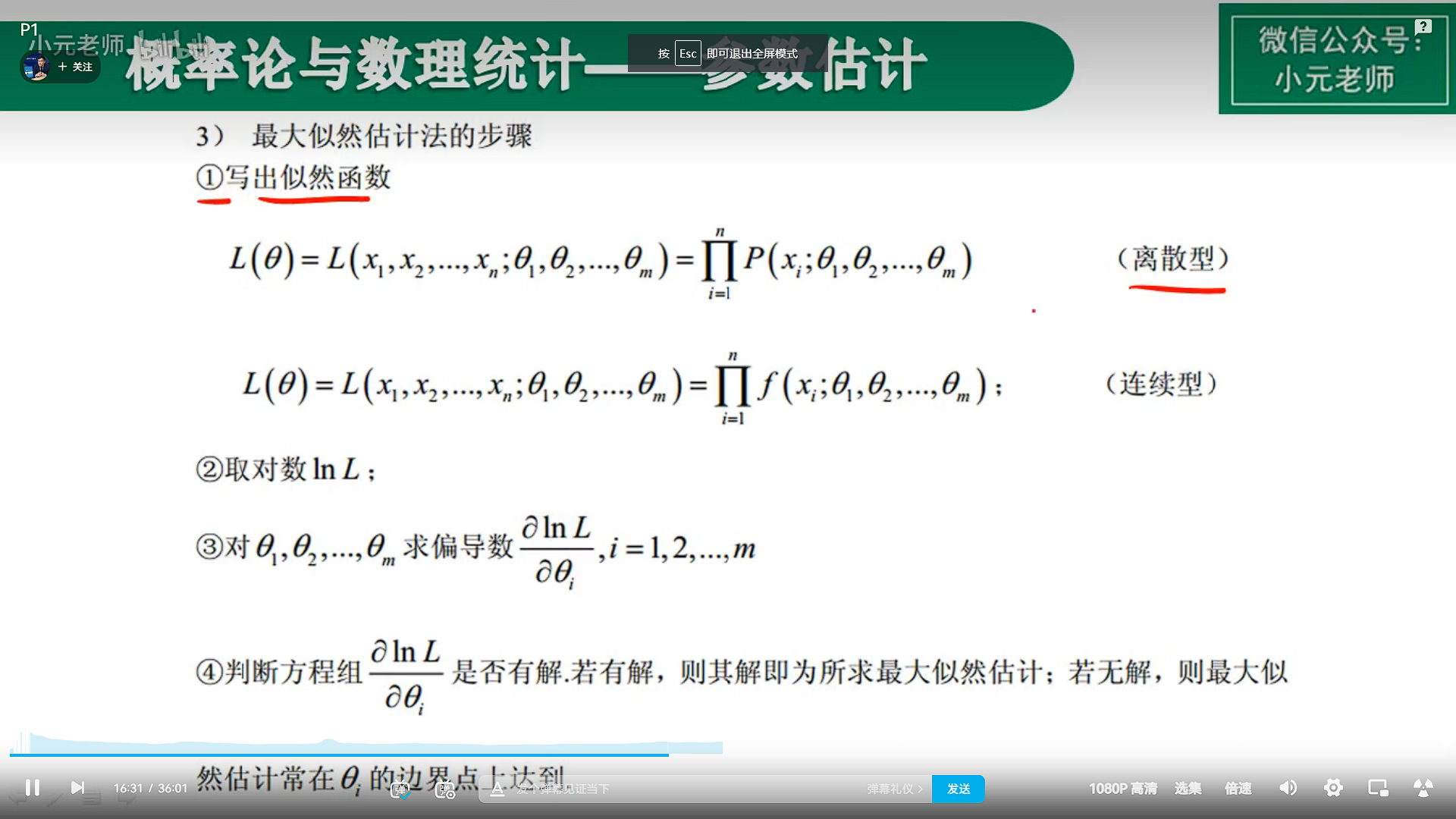
这大概就是我大学高数挂科的原因了吧，高中的我数学算不上好，但也属于能答对最后一道大题的几个人之一吧，但是到了大学，高数最后还是靠老师的施舍才能过。我尤为记着拿到大学考试的时候拿到的高数卷子：这是什么，怎么和课本上的完全不一样啊。我还停留在课本上，但是老师出的已经超出了课本。在看《概率导论》的最后几章节时候，我是看的晕乎转向的，什么是最大似然，为啥取最大？实际意义，或者数学意义在哪？然后不得已，B站找了个视频观看，原来是对应求最大可能性的概率，原来是概率分布下的概率乘数最大化，来计算概率。简单明了，再去翻看书里，隐晦，难懂，上来就是假设，然后公式，没有一点铺垫。所以单单看书本是无法完全理解这些方法的内容的，其实很简单：通过样本数据反推数据发生的概率，通过对数求导，再求和，计算出最大值。反馈到实际意义就是这件事发生的概率。

这算是一个总结吧，要完全理解一个数学概念还是需要刷题，需要看视频，读几本一样的数，不如多刷几道题目，教材一本就够，其他的靠自己刷题理解。